Alfredo Correa, Artur Tamm, Edwin Quashie, Erik Draeger
Collaborators: Andre Schleife (UIUC), Yosuke Kanai (UNC Chapel Hill), Amanda Neukirch (Univ. of Rochester), Anthoty Lim (Imperial College, London), Kyle Reeves (UNC)
Quantum Molecular Dynamics is at the cornerstone of parameter-free materials modelling. In these atomistic models, both the adiabatic Born-Oppenheimer approximation and the thermal equilibrium of the ionic and the electronic subsystems are common approximations. They are justified in most low-energy density and near-equilibrium situations. However, there are very important examples in which one of the subsystems is quickly driven out of equilibrium by an external perturbation.
TDDFT and Ehrenfest Dynamics
Time Dependent Density Functional Theory provides a framework to describe electron dynamics out of the electronic ground state. In particular, Real-time TDDFT provides a non-perturbative description of the electronic excitations upon an external perturbation.
We currently have an implementation of TDDFT and the corresponding electron-ion coupling within the Ehrenfest approximation. The implementation is based on the abinitio planewave pseudopotential code Qbox.
A model system in which this new implementation is being tested is on the problem of electronic stopping, that is the drag generated by electrons on fast ions traversing a material.
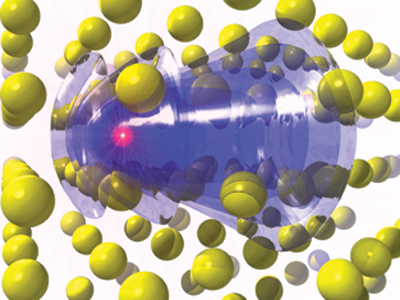
Figure 1: A proton in aluminum crystal generates a wake in the electronic density; conversely electrons stop the fast proton.
Ehrenfest dynamics provides a viable alternative to the usual Born-Oppenheimer Molecular Dynamics in situations where the electronic excitations must be taken into account. Additionally Ehrenfest dynamics overcomes some of the computational limitations of parallelization, as no explicit orthogonalization of wavefunctions is necessary.
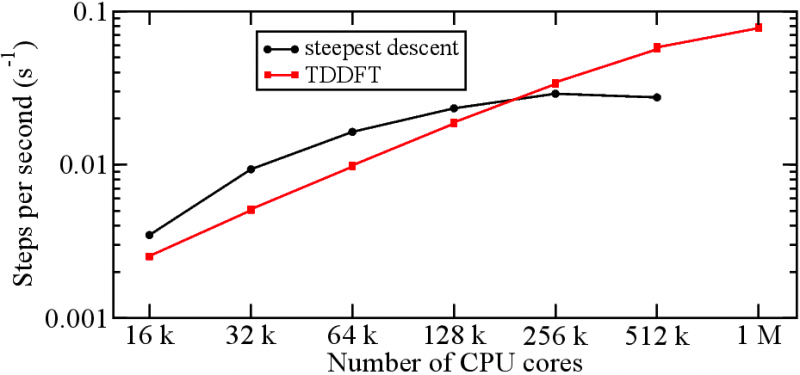
Figure 2: Strong scaling test of TDDFT propagation compared with optimization step (of BOMD) on the Sequoia super computer at LLNL. For small number of processes, propagation is slower than optimization. As the number of processes increase the wall time is reduced, however optimization saturates due to the expensive communication necessary for orthogonalization. Since this is not necessary for propagation, it continues improving with the number of process.
Time-domain Surface Hopping
Electron relaxation is another phenomenon in which the non-adiabatic description of the electron dynamics is important. In its simplest form, adiabatic single-particle electronic states in the conduction band are coupled by the ionic motion (electron-phonon coupling). This non-adiabatic coupling produce a quantum mechanical probability for an excited electron to decay into lower energy state (e.g. at the expense of ionic kinetic energy).
This technique is currently applied to identify electron relaxation times in the context solar energy conversion; as a means to find absorbing system that delay electron-hole recombination as much as possible.
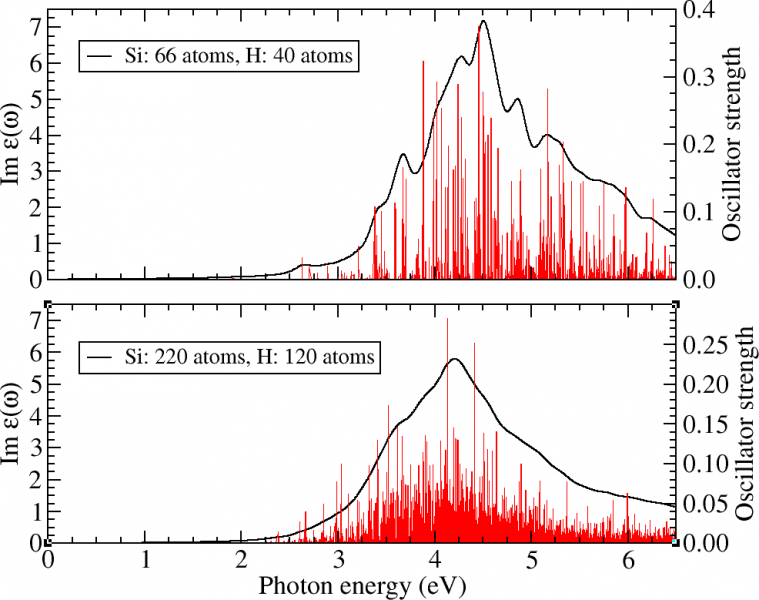
Figure 3. Absorption spectrum of two Hydrogen passivated Silicon quantum dot. After a phonon absorption an electron electron is excited into (few eV) high into the conduction band. The electron eventually relaxes to the bottom of the condition band by electron-phonon coupling (described here by non-adiabatic coupling) in picosecond time scales.
